二叉搜索树的特点

所谓二叉搜索树（Binary Search Tree），又叫二叉排序树，简单而言就是左子树上所有节点的值均小于根节点的值，而右子树上所有节点的值均大于根节点的值，左小右大，并不是乱序，因此又得名二叉排序树。

二叉搜索树要么是空二叉树，要么具有如下特点：

• 二叉搜索树中，如果其根节点有左子树，那么左子树上所有节点的值都小于根节点的值；
• 二叉搜索树中，如果其根节点有右子树，那么右子树上所有节点的值都大小根节点的值；
• 二叉搜索树的左右子树也要求都是二叉搜索树；

有了二叉搜索树，当你要查找一个值，就不需要遍历整个序列或者说遍历整棵树了，可以根据当前遍历到的节点的值来确定搜索方向，这就好比你要去日本，假设你没有见过世界地图，你不知道该往哪个方向走，只能满地球找一遍才能保证一定能够到达日本；而如果你见过世界地图，你知道日本在中国的东边，你就不会往西走、往南走、往北走。这种思维在搜索中被叫做 “剪枝”，把不必要的分枝剪掉可以提高搜索效率。在二叉搜索树中查找值，每次都会把搜索范围缩小，与二分搜索的思维类似。

二叉搜索树的节点定义

二叉搜索树的遍历与二叉树的节点定义一致。

详见：数据结构与算法 - 二叉树的遍历

二叉搜索树的遍历节点

二叉搜索树的遍历与二叉树的遍历方法一致，有三种方法：

• 递归法
• 栈迭代法
• MORRIS 迭代法

详见：数据结构与算法 - 二叉树的遍历

需要注意的是，由于二叉搜索树的特性，在中序遍历二叉搜索树时，节点值会保持递增。

二叉搜索树的查找节点

二叉搜索树中查找某关键字时，查找过程类似于次优二叉树，在二叉搜索树不为空树的前提下，首先将被查找值同树的根节点进行比较，会有 3 种不同的结果：

• 如果相等，查找成功；
• 如果比较结果为根节点的关键字值较大，则说明该关键字可能存在其左子树中；
• 如果比较结果为根节点的关键字值较小，则说明该关键字可能存在其右子树中；

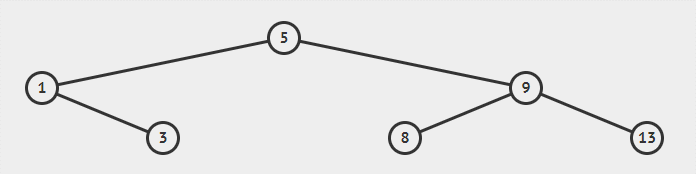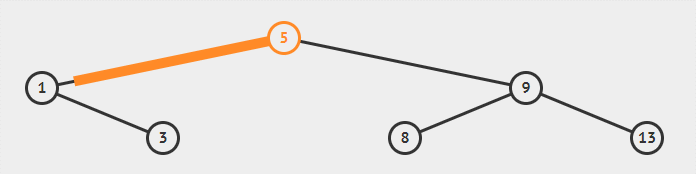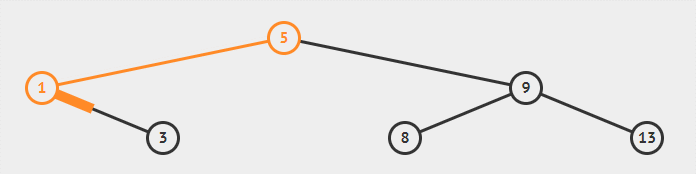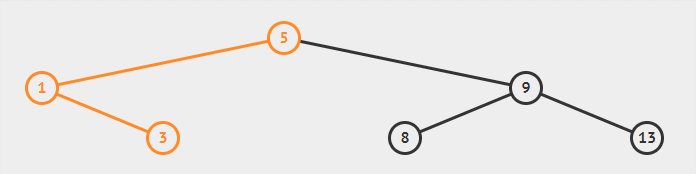
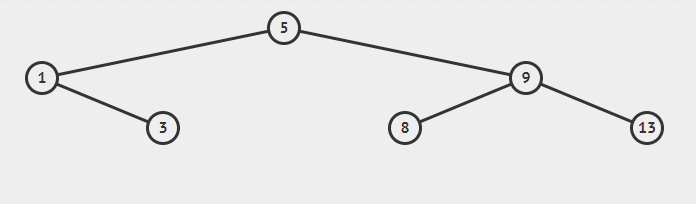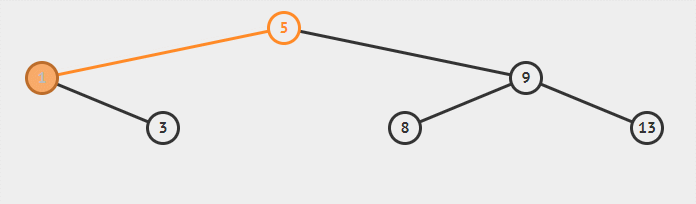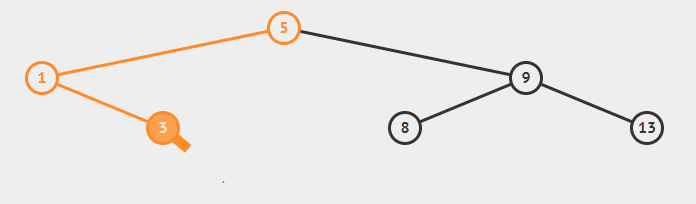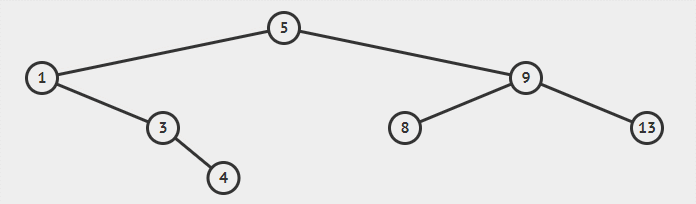
如下图所示的二叉搜索树：

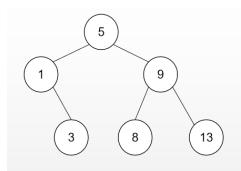
要想查找到 8，则是先到达根节点，其值为 5，8 比 5 大因此继续往右子树上找，到达 9，8 比 9 小因此往左子树上找，最终找到 8；

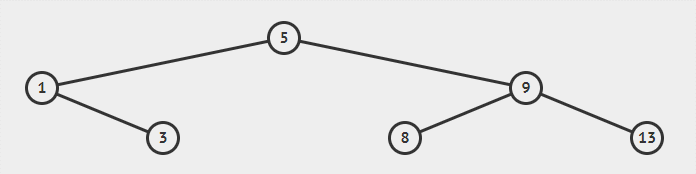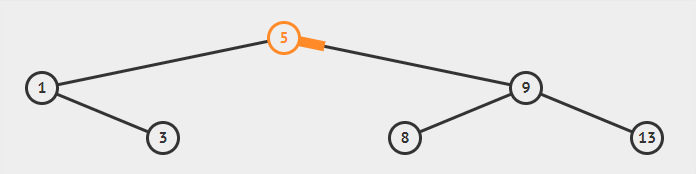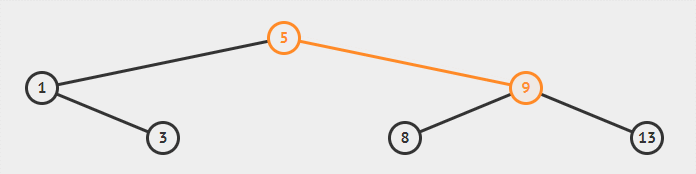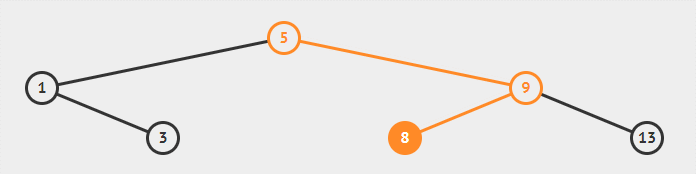
要想查找 4，则是先到达根节点其值为 5，4 比 5 小因此往左子树上找，到达 1，4 比 1 大因此往右子树上找，到达 3，4 比 3 大因此往右子树上找，而值为 3 的节点的右子树是空的，因此该搜索二叉树中不存在值为 4 的节点。

二叉搜索树的插入节点

二叉搜索树本身是动态查找表的一种表示形式，有时会在查找过程中插入或者删除表中元素，当因为查找失败而需要插入数据元素时，该数据元素的插入位置一定位于二叉搜索树的叶子节点，并且一定是查找失败时访问的最后一个节点的左孩子或者右孩子。

例如，在上文的二叉搜索树中做查找 4 的操作，当查找到值 3 所在的叶子节点时，判断出表中没有该值，此时值 4 的插入位置为值 3 的右孩子。

二叉搜索树的删除节点

在查找过程中，如果在使用二叉排序树表示的动态查找表中删除某个数据元素时，需要在成功删除该节点的同时，依旧使这棵树为二叉排序树。

假设要删除的为节点 p，则对于二叉排序树来说，需要根据节点 p 所在不同的位置作不同的操作，有以下 3 种可能：

1. 节点 p 为叶子节点，此时只需要删除该节点，并修改其父节点的指针即可；

   以上文的二叉搜索树中做删除节点 4 的操作为例：

2. 节点 p 只有左子树或者只有右子树

   • 如果 p 是其父节点的左孩子，则直接将 p 节点的左子树或右子树作为其父节点的左子树；
   • 如果 p 是其父节点的右孩子，则直接将 p 节点的左子树或右子树作为其父节点的右子树；

   以上文的二叉搜索树中做删除节点 1 的操作为例：

3. 节点 p 左右子树都有，此时有两种处理方式：

   1. 令节点 p 的左子树为其父节点的左子树；节点 p 的右子树为其自身直接前驱节点的右子树；
   2. 用节点 p 的直接前驱（或直接后继）来代替节点 p，同时在二叉排序树中对其直接前驱（或直接后继）做删除操作。 以上文的二叉搜索树中做删除节点 9 的操作为例，使用直接后继代替了节点 9：