数据结构与算法 - 自平衡二叉搜索树
二叉搜索树的缺陷
二叉搜索树的插入顺序决定了二叉搜索树的结构,如果按照 [1,2,3,4,5,6] 这样的顺序插入,其流程是这样的:

如果在上面的二叉搜索树中查找 6,是要将所有节点都遍历一遍的,时间复杂度就变成了 O(n),几乎就是一个链表。
细心的朋友可能已经发现,插入的序列越接近有序,生成的二叉搜索树就越像一个链表。
为了避免二叉搜索树变成 “链表”,我们引入了自平衡二叉搜索树(平衡二叉树,AVL 树),即让树的结构看起来尽量 “均匀”,左右子树的节点数尽量一样多。
平衡二叉搜索树的特点
平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树(有别于 AVL 算法),且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
平衡二叉搜索树的生成
那给定插入序列,如何生成一棵平衡二叉树呢?
平衡因子
某结点的左子树与右子树的高度 (深度) 差即为该结点的平衡因子(BF,Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。如果某一结点的平衡因子绝对值大于 1 则说明此树不是平衡二叉树。
添加节点
往平衡二叉树中添加节点很可能会导致二叉树失去平衡,所以我们需要在每次插入节点后进行平衡的维护操作。插入节点破坏平衡性有如下四种情况:
- 新加入节点为 node.left 的左孩子, height(node.left) - height(node.right) > 1 。直接对 node 节点右旋。
- 新加入节点为 node.left 的右孩子, height(node.left) - height(node.right) > 1 。这时候要先对 node.left 左旋,调整为 1 的情况,再进行右旋。
- 新加入节点为 node.right 的右孩子, height(node.right) - height(node.left) > 1 。直接对 node 节点左旋。
- 新加入节点为 node.right 的左孩子, height(node.right) - height(node.left) > 1 。这时候要先对 node.right 右旋,调整为 3 的情况,再进行左旋。
要注意的是,节点旋转的时候,高度不是简单的 +/-1,而是要根据从当前节点旋转调整后的左右节点高度中获取较大值 +1。旋转高度调整完成后,返回 node 节点时候,也要重新计算一下新的高度,其高度为左右子树最大值 +1。
LL(右旋)
LL 的意思是向左子树(L)的左孩子(L)中插入新节点后导致不平衡,这种情况下需要右旋操作。
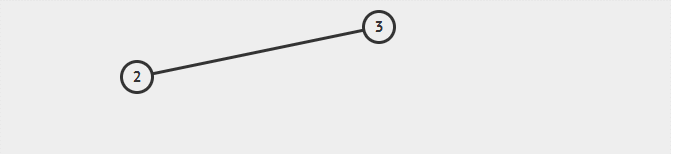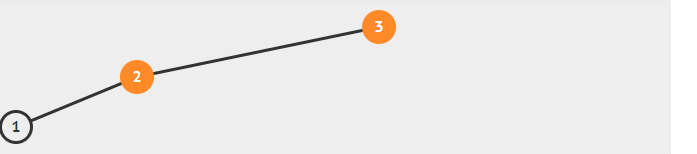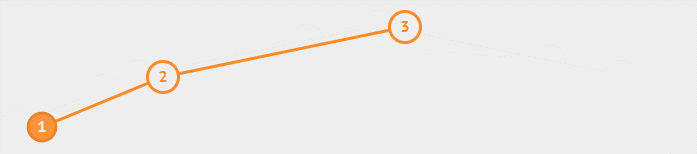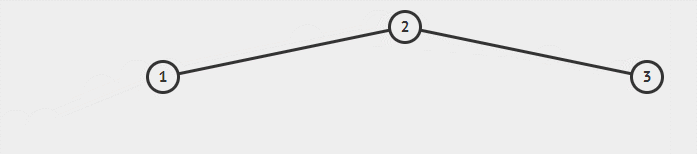
代码示例如下:
/**
* node 节点右旋
* @param node node
* @param nodeHeight node 高度缓存
* @return 旋转后的当前节点
*/
TreeNode* rotateRight(TreeNode* node, map<TreeNode*,int>& nodeHeight) {
// --- 指针调整
TreeNode* left = node->left;
node->left = left->right;
left->right = node;
// --- 高度更新
// 先更新 node 节点的高度,这个时候 node 是 right 节点的左孩子
int newNodeHeight = getCurNodeNewHeight(node, nodeHeight);
nodeHeight[node] = newNodeHeight;
// 更新原 left 节点高度 取现在 right 左右子树最大高度 + 1
nodeHeight[left] = max(newNodeHeight, nodeHeight[left->left]) + 1;
return left;
}
/**
* 获取当前节点的新高度
* @param node node
* @param nodeHeight node 高度缓存
* @return 当前 node 的新高度
*/
private int getCurNodeNewHeight(TreeNode& node, map<TreeNode*,int>& nodeHeight){
// node 节点的高度,为现在 node 左右子树最大高度 + 1
return max(nodeHeight[node.left], nodeHeight[node.right]) + 1;
}RR(左旋)
RR 的意思是向右子树(R)的右孩子(R)中插入新节点后导致不平衡,这种情况下需要左旋操作。

/**
* node 节点左旋
* @param node node
* @param nodeHeight node 高度缓存
* @return 旋转后的当前节点
*/
TreeNode* rotateLeft(TreeNode* node, map<TreeNode*,int>& nodeHeight){
// --- 旋转进行指针调整
TreeNode* right = node->right;
node->right = right->left;
right->left = node;
// --- 高度更新
// 先更新 node 节点的高度,这个时候 node 是 right 节点的左孩子
int newNodeHeight = getCurNodeNewHeight(node, nodeHeight);
nodeHeight[node] = newNodeHeight;
// 取现在 right 左右子树最大高度 + 1 更新原 right 节点高度
nodeHeight[right] = max(newNodeHeight,nodeHeight.getOrDefault(right.right,0)) + 1);
return right;
}