数据结构与算法 - 并查集

发表于 2020-08-29 更新于 2021-11-07 分类于数据结构与算法

并查集介绍

在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合 - 查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union：将两个子集合并成同一个集合。

由于支持这两种操作，一个不相交集也常被称为联合 - 查找数据结构（union-find data structure）或合并 - 查找集合（merge-find set）。

其他的重要方法：

MakeSet，用于创建单元素集合。

有了这些方法，许多经典的划分问题可以被解决。

为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。接着，Find(x) 返回 x 所属集合的代表，而 Union 使用两个集合的代表作为参数。

并查集的实现

并查集森林

并查集森林是一种将每一个集合以树表示的数据结构，其中每一个节点保存着到它的父节点的引用。这个数据结构最早由 Bernard A. Galler 和 Michael J. Fischer 于 1964 年提出，但是经过了数年才完成了精确的分析。

在并查集森林中，每个集合的代表即是集合的根节点。Find 根据其父节点的引用向根行进直到到底树根。Union 将两棵树合并到一起，这通过将一棵树的根连接到另一棵树的根。实现这样操作的一种方法是：

class UnionFind {
private:
    std::vector<int> parent;
public:
    UnionFind(int size) : parent(std::vector<int>(size)) {
        for (int i = 0; i < size; i++)
            parent[i] = i;
    }
    void MakeSet(int x) {
        if (x < parent.size()) parent[x] = x;
        else {
            int osize = parent.size();
            parent.resize(x + 1);
            for (int i = osize; i <= x; i++) parent[i] = i;
        }
    }
    int Find(int x) {
        if (parent[x] == x) return x;
        else return Find(parent[x]);
    }
    void Union(int x, int y) {
        int xRoot = Find(x);
        int yRoot = Find(y);
        parent[xRoot] = yRoot;
    }
};

并查集森林的优化

方法一：按秩合并

“按秩合并”，即总是将更小的树连接至更大的树上。因为影响运行时间的是树的深度，更小的树添加到更深的树的根上将不会增加秩除非它们的秩相同。在这个算法中，术语 “秩” 替代了 “深度”，因为同时应用了路径压缩时（见下文）秩将不会与高度相同。

方法二：路径压缩

第二个优化，称为 “路径压缩”，是一种在执行 “查找” 时扁平化树结构的方法。关键在于在路径上的每个节点都可以直接连接到根上，他们都有同样的表示方法。为了达到这样的效果，Find 递归地经过树，改变每一个节点的引用到根节点。得到的树将更加扁平，为以后直接或者间接引用节点的操作加速。

优化后代码

以上两种方法优化的代码实现如下：

class UnionFind {
private:
    std::vector<int> parent;
    std::vector<int> rank;
public:
    UnionFind(int size) : parent(std::vector<int>(size)) ,rank(std::vector<int>(size)) {
        for (int i = 0; i < size; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
    }
    /* 对 MakeSet 函数进行按秩合并优化 */
    void MakeSet(int x) {
        if (x < parent.size()) parent[x] = x;
        else {
            int osize = parent.size();
            parent.resize(x + 1);
            rank.resize(x + 1);
            for (int i = osize; i <= x; i++) {
                parent[i] = i;
                rank[i] = 0;
            }
        }
    }
    /* 对 Find 函数进行路径压缩优化 */
    int Find(int x) {
        if (parent[x] != x) parent[x] = Find(parent[x]);
        return parent[x];
    }
    /* 对 Union 函数进行按秩合并优化 */
    void Union(int x, int y) {
        int xRoot = Find(x);
        int yRoot = Find(y);
        if (xRoot == yRoot) return;
        if (rank[xRoot] < rank[yRoot]) parent[xRoot] = yRoot;
        else if (rank[xRoot] > rank[yRoot]) parent[yRoot] = xRoot;
        else {parent[yRoot] = xRoot; rank[xRoot]++; }
    }
};

并查集题目解析

684. 冗余连接

684.冗余连接 - 力扣：https://leetcode-cn.com/problems/redundant-connection/

思路：

判断节点第一次出现环的边 edge 进行返回，如下图，当 1 的根节点是 4 的时候，从 1->2->3->41 出现一条路径，大概 [1,4] 这个 edge 进来后，发现 1 可以直接指向 4，这时候出现了环，这条边是冗余边

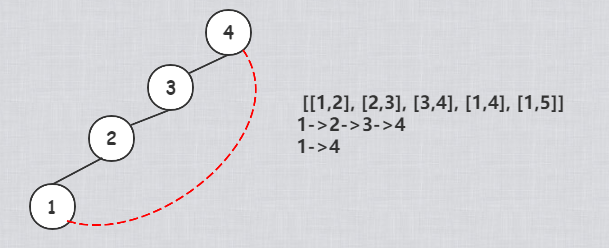
代码实现如下：

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        UnionFind uf(n + 1);
        for(int i = 0; i < n; i++){
            int rootp = uf.Find(edges[i][0]);
            int rootq = uf.Find(edges[i][1]);
            if(rootp == rootq) return edges[i];
            uf.Union(rootp, rootq);
        }
        return {};
    }
};

题目练习

「力扣」第 547 题：省份数量（中等）
「力扣」第 684 题：冗余连接（中等）
「力扣」第 1319 题：连通网络的操作次数（中等）
「力扣」第 1631 题：最小体力消耗路径（中等）
「力扣」第 959 题：由斜杠划分区域（中等）
「力扣」第 399 题：除法求值（中等）
「力扣」第 1202 题：交换字符串中的元素（中等）
「力扣」第 947 题：移除最多的同行或同列石头（中等）
「力扣」第 721 题：账户合并（中等）
「力扣」第 803 题：打砖块（困难）
「力扣」第 1579 题：保证图可完全遍历（困难）
「力扣」第 778 题：水位上升的泳池中游泳（困难）

何照江的博客