编解码技术：H264 - 描述符 & 熵编码

发表于 更新于 分类于

描述符介绍

描述符描述了从比特流提取句法元素的方法，即句法元素的解码算法，每个句法元素都有相对应的描述符。由于 H.264 编码的最后一步是熵编码，所以这里的描述子大多是熵编码的解码算法。H.264 定义了如下几种描述符：

  • ae(v)：基于上下文自适应的二进制算术熵编码
  • b(8)：任意形式的 8 比特字节
  • ce(v)：基于上下文自适应的可变长熵编码语法元素，左位在先
  • f(n)：n 位固定模式比特串，左位在先
  • i(n)/i(v)：n 比特的有符号整数，如果是 i(v)，其比特数由其它语法元素值确定
  • me(v)：映射指数哥伦布熵编码的语法元素，左位在先
  • se(v)：有符号整数指数哥伦布熵编码的语法元素，左位在先
  • te(v)：截断指数哥伦布熵编码语法元素，左位在先
  • u(n)/u(v)：n 位无符号整数，如果是 u(v)，其比特数由其它语法元素值确定
  • ue(v)：无符号整数指数哥伦布编码的语法元素，左位在先

从上述列表中看出，大部分的描述符采用了熵编码进行编码，所以我们主要讨论其中涉及到的熵编码方式：

  • 指数哥伦布熵编码（Exp-Golomb code）
    • 无符号整数指数哥伦布编码（unsigned integer Exp-Golomb-code）
    • 有符号整数指数哥伦布熵编码（signed integer Exp-Golomb-code）
    • 映射指数哥伦布熵编码（mapped Exp-Golomb-code）
    • 截断指数哥伦布熵编码（truncated Exp-Golomb-code）
  • 基于上下文自适应的二进制算术熵编码（CABAC）
  • 基于上下文自适应的可变长熵编码（CAVLC）

熵编码

熵编码压缩是一种无损压缩，其实现原理是使用新的编码来表示输入的数据，从而达到压缩的效果。常用的熵编码有游程编码，哈夫曼编码和 CAVLC 编码等。

Exp-Golomb-code

指数哥伦布码（Exponential-Golomb coding）是一种无损数据压缩方法。

用来表示非负整数的 k 阶指数哥伦布码可用如下步骤生成：

  1. 将数字以二进制形式写出 (B)，去掉最低的 k 个比特 (D)，之后加 1 (A = B + 1)
  2. 计算 A 的比特个数 (C)，将此数减一，即是需要增加的前导零个数 (Z = C -1)
  3. 将第一步中去掉的最低 k 个比特位补回比特串尾部 (ExpG = Z 个 0 + A + D)

0 阶指数哥伦布编码如下所示：

    Step 1                            Step 2            Step 3
0   => B = 0,    D = None, A = 1      => C = 1, Z = 0   => 1
1   => B = 1,    D = None, A = 10     => C = 2, Z = 1   => 010
2   => B = 10,   D = None, A = 11     => C = 2, Z = 1   => 011
3   => B = 11,   D = None, A = 100    => C = 3, Z = 2   => 00100
4   => B = 100,  D = None, A = 101    => C = 3, Z = 2   => 00101
5   => B = 101,  D = None, A = 110    => C = 3, Z = 2   => 00110
6   => B = 110,  D = None, A = 111    => C = 3, Z = 2   => 00111
7   => B = 111,  D = None, A = 1000   => C = 4, Z = 3   => 0001000
8   => B = 1000, D = None, A = 1001   => C = 4, Z = 3   => 0001001
9   => B = 1001, D = None, A = 1010   => C = 4, Z = 3   => 0001010

以数字 9 为例：

  1. 2 进制值 B 为 1001, 因为 K 为 0 阶，去除 0 个比特，故 D 值为 None，把 B 值加 1 得到 A，值为 1010
  2. 计算 A 的比特个数，得到 C 值为 4，故减 1 后得到前导零 Z , 值为 3
  3. 最后组合 Z + A + D 之后，得到 000 + 1010 + None ，故 Exp-G 值为 0001010

1 阶指数哥伦布编码如下所示：

      Step 1                        Step 2            Step 3
0   => B = 0,    D = 0, A = 1     => C = 1, Z = 0   => 10
1   => B = 1,    D = 1, A = 1     => C = 1, Z = 0   => 11
2   => B = 10,   D = 0, A = 10    => C = 2, Z = 1   => 0100
3   => B = 11,   D = 1, A = 10    => C = 2, Z = 1   => 0101
4   => B = 100,  D = 0, A = 11    => C = 2, Z = 1   => 0110
5   => B = 101,  D = 1, A = 11    => C = 2, Z = 1   => 0111
6   => B = 110,  D = 0, A = 100   => C = 3, Z = 2   => 001000
7   => B = 111,  D = 1, A = 100   => C = 3, Z = 2   => 001001
8   => B = 1000, D = 0, A = 101   => C = 3, Z = 2   => 001010
9   => B = 1001, D = 1, A = 101   => C = 3, Z = 2   => 001011

unsigned integer Exp-Golomb-code

H264 编码中无符号整数指数哥伦布编码即为标准 0 阶指数哥伦布编码方式：

  • 编码过程： > 编码过程与 0 阶指数哥伦布编完全相同

  • 解码过程：

    1. 获取开头 0 字节的个数 leadingZeroBits：

       leadingZeroBits = -1;
 for(b = 0; !b; leadingZeroBits++)
     b = read_bits(1)

    2. 计算编码前数字 unsigncodeNum：

       unsigncodeNum = 2 ^ leadingZeroBits − 1 + read_bits(leadingZeroBits)
 注：read_bits(leadingZeroBits) 的返回值使用高位在先的二进制无符号整数表示。

    例如：解码 0001010 过程如下：

      1.  read_bits 指向解码二进制流开头：0 001010
      获取开头 0 字节的个数：leadingZeroBits = 3
      此时 read_bits 指向了二进制流中首个 1 的后一位：0001 0 10
  2.  read_bits(leadingZeroBits) = read_bits(3) = 010 = 2
      unsigncodeNum = 2 ^ 3 - 1 + 2 = 9

  • 如果语法元素编码为 te(v)，首先应该判断语法元素的范围。语法元素的范围可以是在 0 和 x 之间，x 大于或者等于 1，语法元素的值按照如下方法取得：

    • 如果 x 大于 1，codeNum 和语法元素值的取得应该和 ue(v) 相同。
    • 否则 (x 等于 1)，与语法元素值相等的 codeNum 的解析过程由如下计算方法取得：

signed integer Exp-Golomb-code

  • 编码过程：

  • 如果待编码数据为非正整数，则将待编码数据乘 -2 后进行无符号整数指数哥伦布编码

  • 如果待编码数据为正整数，则将待编码数据乘 2 并减 1 后进行无符号整数指数哥伦布编码

有符号整数指数哥伦布熵编码如下所示：

    0   ⇒ 0   ⇒ 1      ⇒ 1
    1   ⇒ 1   ⇒ 10     ⇒ 010
   −1   ⇒ 2   ⇒ 11     ⇒ 011
    2   ⇒ 3   ⇒ 100    ⇒ 00100
   −2   ⇒ 4   ⇒ 101    ⇒ 00101
    3   ⇒ 5   ⇒ 110    ⇒ 00110
   −3   ⇒ 6   ⇒ 111    ⇒ 00111
    4   ⇒ 7   ⇒ 1000   ⇒ 0001000
   −4   ⇒ 8   ⇒ 1001   ⇒ 0001001
  • 解码过程

可以通过简单的计算将 unsigned integer Exp-Golomb-code 得出的 unsigncodeNum 转换为 signedcodeNum：

signedcodeNum = (-1) ^ unsigncodeNum * ⌈ unsigncodeNum ÷ 2 ⌉

mapped Exp-Golomb-code

可以通过下表将 unsigned integer Exp-Golomb-code 得出的 unsigncodeNum 映射为 mapcodeNum（）：

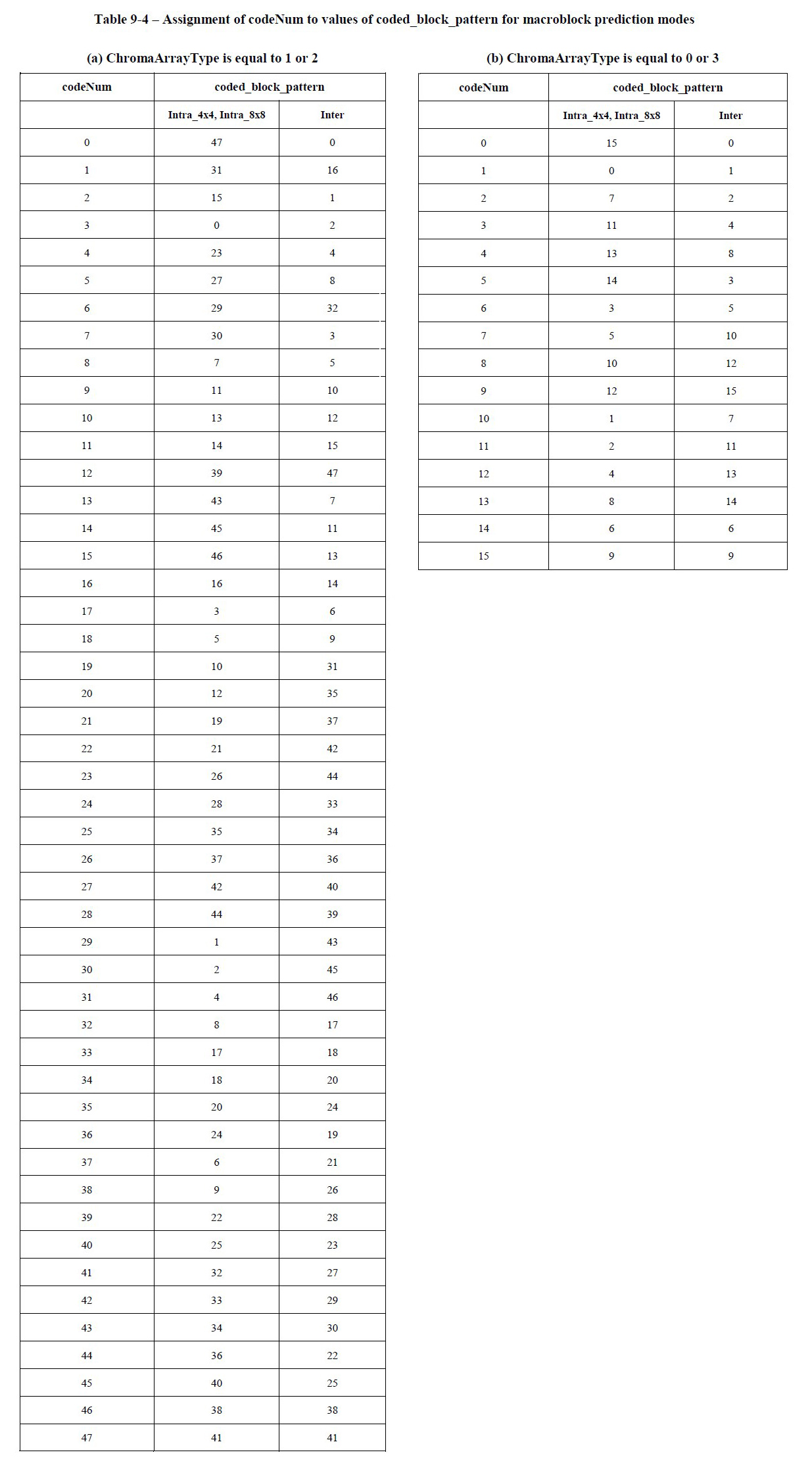
Assignment of codeNum to values of coded_block_pattern for macroblock prediction modes

truncated Exp-Golomb-code

  • 编码过程

截断指数哥伦布熵编码在编码时先判断待编码值的取值范围的上限 x：

  • 如果 x 大于 1，则用 ue(v) 规则直接编码。

  • 如果 x 等于 1，则待编码值为 1 编码后的值为 0，待编码的值为 0 编码后的值为 1。

  • 解码过程

解码时先判断待编码值的取值范围的上限 x：

  • 如果 x 大于 1，则用 ue(v) 规则直接解码。
  • 如果 x 等于 1，则待解码值为 1 解码后的值为 0，如果待解码的值为 0 解码后的值为 1。

CABAC

CABAC(ContextAdaptive Binary Arithmatic Coding) 是 H.264/MPEG-4AVC 中使用的熵编码算法。CABAC 在不同的上下文环境中使用不同的概率模型来编码。其编码过程大致是这样：首先，将欲编码的符号用二进制 bit 表示；然后对于每个 bit，编码器选择一个合适的概率模型，并通过相邻元素的信息来优化这个概率模型；最后，使用算术编码压缩数据。

详见：编解码技术：H264 - CABAC

CAVLC

CAVLC(Context Adaptive VariableLength Coding) 是在 H.264/MPEG-4AVC 中使用的熵编码方式。在 H.264 中，CAVLC 以 zig-zag 顺序用于对变换后的残差块进行编码。CAVLC 是 CABAC 的替代品，虽然其压缩效率不如 CABAC，但 CAVLC 实现简单，并且在所有的 H.264 profile 中都支持。

详见：编解码技术：H264 - CABVLC

参考资料