在 H264 编码预测时，选择哪种预测方式是一个永远躲避不了的一个问题，我们希望找到一个最优的预测方式，即预测的亮度 / 色度值与真实的亮度 / 色度值最为接近。这就需要有一种计算方法来评价各种预测方式的效果，我们称这种计算方法为代价计算。

常用代价计算函数

SAD

SAD(Sum of Absolute Difference) 也可以称为 SAE(Sum of Absolute Error)，即绝对误差和。它的计算方法就是求出两个像素块对应像素点的差值，将这些差值分别求绝对值之后再进行累加。

SSD

SSD(Sum of Squared Difference) 也可以称为 SSE(Sum of Squared Error)，即差值的平方和。它和 SAD 的区别在于多了一个平方。

SATD

SATD(Sum of Absolute Transformed Difference) 即 Hadamard 变换后再绝对值求和。它和 SAD 的区别在于多了一个变换。

Hadamard 变换

阿达马变换（Hadamard transform），是一种广义傅立叶变换，作为变换编码的一种在影片编码当中使用有很久的历史。在近来的影片编码标准中，阿达马变换多被用来计算 SATD

变换矩阵

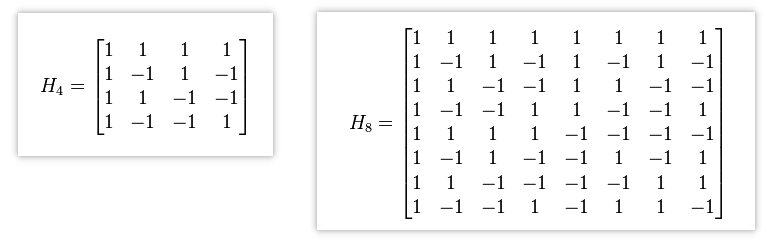
在 H.264 中使用了 4 阶和 8 阶的阿达马变换来计算 SATD，其变换矩阵为：

SATD 计算方法

当计算 4x4 块 \(\begin{bmatrix}L_4\end{bmatrix}\) 的 SATD 时，先使用下面的方法进行二维的 Hadamard 变换

\[ \begin{bmatrix}L_4'\end{bmatrix} = \begin{bmatrix}H_4\end{bmatrix} \times \begin{bmatrix}L_4\end{bmatrix} \times \begin{bmatrix}H_4\end{bmatrix} \]

然后计算 \(\begin{bmatrix}L_4'\end{bmatrix}\) 所有系数绝对值之和并归一化。

类似的，当计算 8x8 块 \(\begin{bmatrix}L_8\end{bmatrix}\) 的 SATD 时，先使用下面的方法进行二维的 Hadamard 变换：

\[ \begin{bmatrix}L_8'\end{bmatrix} = \begin{bmatrix}H_8\end{bmatrix} \times \begin{bmatrix}L_8\end{bmatrix} \times \begin{bmatrix}H_8\end{bmatrix} \]

然后计算 \(\begin{bmatrix}L_8'\end{bmatrix}\) 所有系数绝对值之和并归一化。

H.264 中的代价计算函数选择

H.264 中使用 SAD 和 SATD 进行宏块预测模式的判断。早期的编码器使用 SAD 进行计算，近期的编码器多使用 SATD 进行计算。

为什么使用 SATD 而不使用 SAD 呢？关键原因在于编码之后码流的大小是和图像块 DCT 变换后频域信息紧密相关的，而和变换前的时域信息关联性小一些。SAD 只能反应时域信息；SATD 却可以反映频域信息，而且计算复杂度也低于 DCT 变换，因此是比较合适的模式选择的依据。

使用 SAD 进行模式选择的示例如下所示。下面这张图代表了一个普通的 Intra16x16 的宏块的像素。它的下方包含了使用 Vertical，Horizontal，DC 和 Plane 四种帧内预测模式预测的像素。通过计算可以得到这几种预测像素和原始像素之间的 SAD(SAE) 分别为 3985，5097，4991，2539。由于 Plane 模式的 SAD 取值最小，由此可以断定 Plane 模式对于这个宏块来说是最好的帧内预测模式。