数据压缩技术 - 算术编码
算术编码的原理
算术编码是 1980 年代发展起来的一种熵编码方法。
基本原理是将被编码的数据序列表示成 0 和 1 之间的一个间隔 (也就是一个小数范围),该间隔的位置与输入数据的概率分布有关。信息越长,编码表示的间隔就越小,因而表示这一间隔所需的二进制位数就越多 (由于间隔是用小数表示的)。
算术编码的步骤
算数编码是从整个符号序列出发,采用递推式连续编码的方法。解码时,根据该区间判断信源各个符号出现的顺序和类型。
下面以一个多符号的算术编码为例来分析算术编码的步骤:
例: 对一个简单的信号源进行观察,得到的统计模型如下:
- 60% 的机会出现符号 \(a_{1}\)
- 20% 的机会出现符号 \(a_{2}\)
- 10% 的机会出现符号 \(a_{3}\)
- 10% 的机会出现符号 数据结束符 \(a_{4}\) (出现这个符号的意思是该信号源'内部中止',在进行数据压缩时这样的情况是很常见的。当第一次也是唯一的一次看到这个符号时,解码器就知道整个信号流都被解码完成了)。
解:
- 首先定义算法空间为 [0 1]。
- 确定各个字符的区间分配,建立码点,码点要满足如下两条规则:
- 每一个码点值是它前面所出现的概率之和;(第一个码点值是 0,因为它之前没有码字;第一个符号 \(a_{1}\) 出现的概率为 0.6,故第二个码点值是 0.6,依次类推。)
- 将每一个码点值作为右端点,每个子分过程中所得区间的宽度对应于该符号的概率。
- \(a_{1}\) 对应的区间是 [0, 0.6)
- \(a_{2}\) 对应的区间是 [0.6, 0.8)
- \(a_{3}\) 对应的区间是 [0.8, 0.9)
- 数据结束符 \(a_{4}\) 对应的区间是 [0.9, 1)
- 对输入的每个信源符号,重复如下步骤:
- 将第一个信源符号 \(a_{1}\) 出现的概率空间 [0 0.6) 扩展为新的算法子空间,将当前区间分割为长度正比于信源集内各个符号概率的区间;
- 接下来确定第二个符号是 \(a_{3}\) 的子区间,即序列 \(a_{1},a_{3}\) 的子区间:
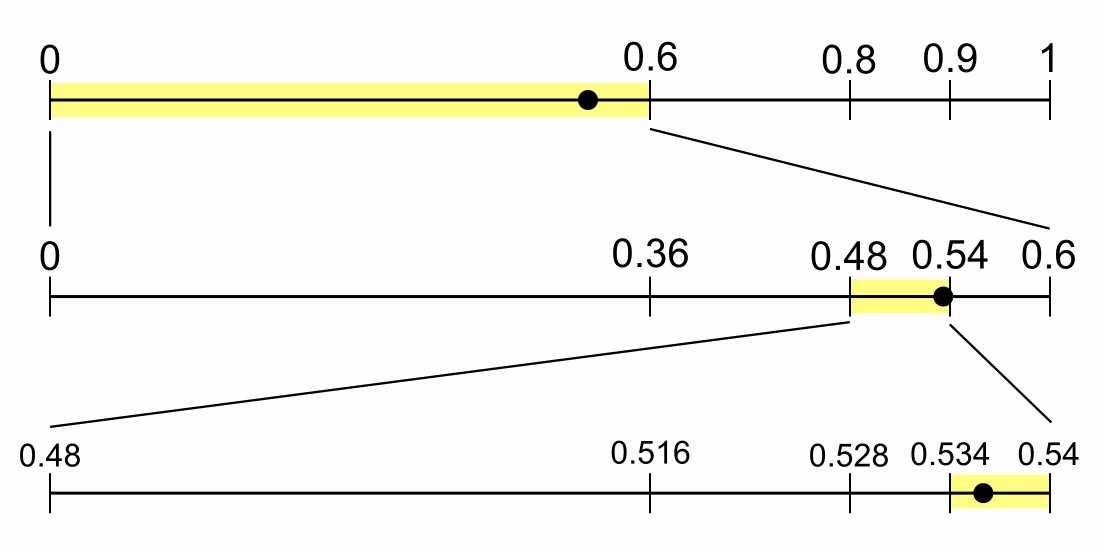
比如要编码序列 \(a_{1},a_{3},a_{4}\):
- 读入 \(a_{1}\),结果区间为 [0, 0.6)
- 读入 \(a_{3}\),结果区间为 [0 + 0.6 * 0.8, 0 + 0.6 * 0.9) = [0.48, 0.54)
- 读入 \(a_{4}\),结果区间为 [0.48 + 0.06 * 0.9, 0.48 + 0.06 * 1) = [0.534, 0.54)
当所有的符号都编码完毕,最终得到的结果区间即唯一的确定了已编码的符号序列。任何人使用该区间和使用的模型参数即可以解码重建得到该符号序列。
实际上我们并不需要传输最后的结果区间 [0.534, 0.54),实际上,我们只需要传输该区间中的一个小数(比如 0.535)即可。在实用中,只要传输足够的该小数足够的位数(不论几进制),以保证以这些位数开头的所有小数都位于结果区间就可以了。
算术解码的步骤
例: 下面对使用前面提到的 4 符号模型进行编码的一段信息进行解码。编码的结果是 0.538(为了容易理解,这里使用十进制而不是二进制;我们也假设我们得到的结果的位数恰好够我们解码。下面会讨论这两个问题)。
像编码器所作的那样我们从区间 [0,1) 开始,使用相同的模型,我们将它分成编码器所必需的四个子区间。分数 0.538 落在 \(a_{1}\) 坐在的子区间 [0,0.6);这向我们提示编码器所读的第一个符号必然是 \(a_{1}\),这样我们就可以将它作为消息的第一个符号记下来。
然后我们将区间 [0,0.6) 分成子区间:
- \(a_{1}\) 的区间是 [0, 0.36) -- [0, 0.6) 的 60%
- \(a_{2}\) 的区间是 [0.36, 0.48) -- [0, 0.6) 的 20%
- \(a_{3}\) 的区间是 [0.48, 0.54) -- [0, 0.6) 的 10%
- 数据结束符 \(a_{4}\) 的区间是 [0.54, 0.6). -- [0, 0.6) 的 10%
0.538 在 [0.48, 0.54) 区间;所以消息的第二个符号一定是 \(a_{3}\)。
我们再一次将当前区间划分成子区间:
- \(a_{1}\) 的区间是 [0.48, 0.516)
- \(a_{2}\) 的区间是 [0.516, 0.528)
- \(a_{3}\) 的区间是 [0.528, 0.534)
- 数据结束符 \(a_{4}\) 的区间是 [0.534, 0.540)
0.538 落在符号数据结束符 \(a_{4}\) 的区间;所以,这一定是下一个符号。由于它也是内部的结束符号,这也就意味着编码已经结束。(如果数据流没有内部结束,我们需要从其它的途径知道数据流在何处结束,否则我们将永远将解码进行下去,错误地将不属于实际编码生成的数据读进来。)
同样的消息能够使用同样短的分数来编码实现如 0.534、0.535、0.536、0.537 或者是 0.539,这表明使用十进制而不是二进制会带来效率的降低。这是正确的是因为三位十进制数据能够表达的信息内容大约是 9.966 位;我们也能够将同样的信息使用二进制分数表示为 0.10001010(等同于 0.5390625),它仅需 8 位。这稍稍大于信息内容本身或者消息的信息熵,大概是概率为 0.6% 的 7.361 位信息熵。(注意最后一个 0 必须在二进制分数中表示,否则消息将会变得不确定起来。)
算术编码的分析
算术编码是一种从整个符号系列出发,采用递推形式连续编码的方法。在算术编码中,字母表中的符号和码字间不再存在一一对应关系,一个算术码字要赋给整个信源符号序列(即不是一次编一个号),而码字本身确定 0 和 1 之间的一个实数区间。
不论是否是二元信源,也不论数据的概率分布如何,其平均码长均能逼近信源的熵。
算术编码和霍夫曼编码的区别就在于:在算术编码中,输入序列(即被赋给单个码字的符号块)的长度,是可变的,可以说,算术编码是将可变长码字赋给可变长符号块
正是由于算术编码不需要为定长符号块分配整数长的码字,理论上能达到无损编码定理所规定的最低限。
在编码过程中,尽管在计算时有乘法运算,但可以通过移位实现,即通过加法和移位实现算术运算。在解码时,要除以符号区间概率,也可以通过移位实现,即通过减法和移位实现算术解码。这正是把这种编码方法称为算术码的原因。
算术编码从全序列出发,采用递推形式的连续编码,它不是将单个的信源符号映射成一个码字,而是将整个符号序列映射为实数轴上 [0,1)区间内的一个小区间,其长度等于该序列的概率。
随着输入符号越来越多,子区间分割越来越精细,因此表示其左端点的数值的有效位数也越来越多。
如果等整个符号序列输入完毕后再将最终得到的左端点输出,将遇到两个问题:第一,当符号序列很长时,将不能实时编解码;第二,有效位太长的数难以表示。
为了解决这个问题,通常采用两个有限精度的移位寄存器存放码字的最新部分,随着序列中符号的不断输入,不断地将其中的高位移出到信道上,以实现实时编解码。
算术编码的效率
算术编码的最大优点之一在于它具有自适应性和高编码效率。
算术编码的模式选择直接影响编码效率。其模式有固定模式和自适应模式两种:
- 固定模式是基于概率分布模型进行编码。
- 自适应模式中,其各符号的初始概率都相同,但会随着符号顺序的出现而改变各符号的概率。
在无法进行信源概率模型统计的条件下,非常适于使用自适应模式的算术编码。
在信道符号概率比较均匀的情况下,算术编码的编码效率高于 Huffman 编码。但在实现上,比 Huffman 编码的计算过程复杂。
算术码也是变长码,编码过程中的移位和输出都不均匀,需要有缓冲存储器。
在误差扩散方面,也比分组码更严重。在分组码中,由于误码而破坏分组,过一段时间后常能自动恢复;但在算术码中,却往往会一直延续下去,因为它是从全序列出发来编码的。因而算术码流的传输也要求高质量的信道,或采用检错反馈重发的方式。