数据结构与算法 - 欧拉回路 & 通路
欧拉回路 & 通路介绍
一笔画问题
一笔画问题:给定一个 n 个点 m 条边的图,要求从指定的顶点出发,经过所有的边恰好一次。
欧拉回路 & 通路与一笔画问题的关系
定义:
- 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路。
- 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路。
- 注:定义中边经过且仅经过 1 次,顶点的经过次数不受限制。
欧拉图 & 半欧拉图
定义:
- 具有欧拉回路的图称为 欧拉图。
- 具有欧拉通路但不具有欧拉回路的图称为 半欧拉图。
欧拉图 & 半欧拉图的判别
如果没有保证至少存在一种合理的路径,我们需要判别这张图是否是欧拉图或者半欧拉图,具体地:
- 对于无向图 G,G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。
- 对于无向图 G,G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 2 个奇度顶点。
- 对于有向图 G,G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
- 对于有向图 G,G 是半欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且
- 恰有一个顶点的出度与入度差为 1;
- 恰有一个顶点的入度与出度差为 1;
- 所有其他顶点的入度和出度相同。
从上述描述中可知,如果图 G 是一个连通图,则可用如下表格判断其是否是欧拉图 / 半欧拉图:
| 欧拉图(具有欧拉回路) | 半欧拉图(欧拉通路) | |
|---|---|---|
| 无向图 | 所有顶点都是偶度 | 所有顶点都是偶度或有且仅有两个奇度节点 |
| 有向图 | 所有节点的出度和入度均相同 | 有且仅有一个顶点的出度减入度等于 1 有且仅有一个顶点的入度减出度等于 1 所有其他顶点的入度和出度相同 |
Code332 重新安排行程
332: 重新安排行程 - 力扣 https://leetcode-cn.com/problems/reconstruct-itinerary/
将该题转化为一笔画问题:给定一个 n 个点 m 条边的图,要求从指定的顶点出发,经过所有的边恰好一次,且使得路径的字典序最小。
Hierholzer 算法
Hierholzer 算法用于在连通图中寻找欧拉路径,其流程如下:
- 从起点出发,进行深度优先搜索。
- 每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边。
- 如果没有可移动的路径,则将所在节点加入到栈中,并返回。
当我们顺序地考虑该问题时,我们也许很难解决该问题,因为我们无法判断当前节点的哪一个分支是「死胡同」分支。
不妨倒过来思考。我们注意到只有那个入度与出度差为 1 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则,当我们遍历完一个节点所连的所有节点后,我们才将该节点入栈(即逆序入栈)。
对于当前节点而言,从它的每一个非「死胡同」分支出发进行深度优先搜索,都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。
这样就能保证我们可以「一笔画」地走完所有边,最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转,即可得到答案。
另外,为了保证我们能够快速找到当前节点所连的节点中字典序最小的那一个,我们可以使用优先队列存储当前节点所连到的点,每次我们 O(1) 地找到最小字典序的节点,并 O(logm) 地删除它。
C++ 代码实现如下:
class Solution {
public:
unordered_map<string, priority_queue<string, vector<string>, std::greater<string>>> vec;
vector<string> stk;
void dfs(const string& curr) {
while (vec.count(curr) && vec[curr].size() > 0) {
string tmp = vec[curr].top();
vec[curr].pop();
dfs(move(tmp));
}
stk.emplace_back(curr);
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (auto& it : tickets) {
vec[it[0]].emplace(it[1]);
}
dfs("JFK");
reverse(stk.begin(), stk.end());
return stk;
}
};Code753 破解保险箱
753: 破解保险箱 - 力扣 https://leetcode-cn.com/problems/cracking-the-safe/
题目描述:
有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位是 k 位序列 0, 1, ..., k-1 中的一个。
你可以随意输入密码,保险箱会自动记住最后 n 位输入,如果匹配,则能够打开保险箱。
举个例子,假设密码是 "345",你可以输入 "012345" 来打开它,只是你输入了 6 个字符.
请返回一个能打开保险箱的最短字符串。
算法思想
这道题说的是给了 k 个数字,值为 0 到 k-1,让我们组成 n 位密码。我们可以发现,为了尽可能的使钥匙串变短,所以我们的密码之间尽可能要相互重叠:
- 如果密码是 2 位数,00 和 001 共享一个数 0,可以用来解锁密码为 00 和 01 的两个保险箱
- 如果密码是 3 个数,012 和 0120 共享两个数 12,可以用来解锁密码为 012 和 120 的两个保险箱
我们可以发现,两个长度为 n 的密码最好能共享 n-1 个数字,这样累加出来的钥匙串肯定是最短的。
密码共有 n 位,每一个位可以有 k 个数字,那么总共不同的密码总数就有 kn 个,而每个密码可以公用 n - 1 位,所以破解保险箱的密码最短长度为:n - 1 + kn 位。
我们可以考虑创建一个有 kn-1 个节点的图,每个节点有 k 条出边,则该图中一共有 kn 条边,将【节点代表的 n - 1 位数字 + 边代表的 1 位数字】作为经过该条边后尝试的密码值,而经过边后到达的新节点代表的 n - 1 位数字,可以作为下一个密码的前 n - 1 位数字使用,这样可以保证每个密码值不重复,又完全覆盖了 kn 个密码值。
以三位密码的二进制保险箱(n = 3, k = 2)举例:
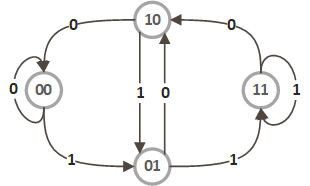
我们可以按如下顺序遍历图中所有的边:
00 -> 00 -> 01 -> 11 -> 11 -> 10 -> 01 -> 10 -> 00
00 0 1 1 1 0 1 0 0 --> 0011101000最后可得出破解该保险箱的最短字符顺序为:0011101000,其位数也正好为 n - 1 + kn = 3 - 1 + 23 = 10 位。
将其拓展为 n 位 k 个数字的密码:比如节点为 a1a2a3...an 经过边 am 后的新节点为 a2a3...anam。
仍利用 Hierholzer 算法:
- 从起点(以 n - 1 个 0 的节点作为起点,当然也可以选择其他节点)出发,进行深度优先搜索。
- 每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边(标记该条边已经过)。
- 如果没有可移动的路径,则将所在节点加入到字符串中,并返回。
class Solution {
public:
int node = 0;
void dfs(vector<int> & side, int n, int k, int i, string& res) {
int currNode = i % node;
for (int j = 0; j < k; ++j) {
int t = currNode * k + j;
if (!side[t]++) { /* 仅遍历没有走过的边 */
dfs(side, n, k, t, res);
res += j + '0';
}
}
}
string crackSafe(int n, int k) {
node = pow(k, n - 1); /* 节点个数 */
vector<int> side(node * k, 0); /* 边数个标志,用来指示每条边是否遍历过 */
string res;
dfs(side, n, k, 0, res); /* 从 n -1 个 0 的节点开始寻找 */
res.append(n - 1, '0'); /* 补充起始节点字符串 */
return res; /* 无需 reverse,翻转前后均为正确答案 */
}
};