数据结构与算法 - 拓扑排序
「先穿袜子,再穿鞋子」 --- 这就是一种拓扑排序
首先声明:拓扑排序并不是通常意义上的【排序】算法
拓扑排序简介
给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足:
对于图 G 中的任意一条有向边 (u,v),u 在排列中都出现在 v 的前面。那么称该排列是图 G 的「拓扑排序」。根据上述的定义,我们可以得出两个结论:
如果图 G 中存在环,那么图 G 不存在拓扑排序(即只有「有向无环图」存在拓扑排序)
如果图 G 是有向无环图,那么它的拓扑排序可能不止一种
在很多应用中, 有向无回路图用于说明事件发生的先后次序, 下图给出了一个实例,说明 Bumstead 教授早晨穿衣的过程。他必须先穿好某些衣服, 才能再穿其他衣服(如先穿袜子后才能穿鞋) , 其他的一些衣服前可以按任意次序穿戴(如袜子和裤子)
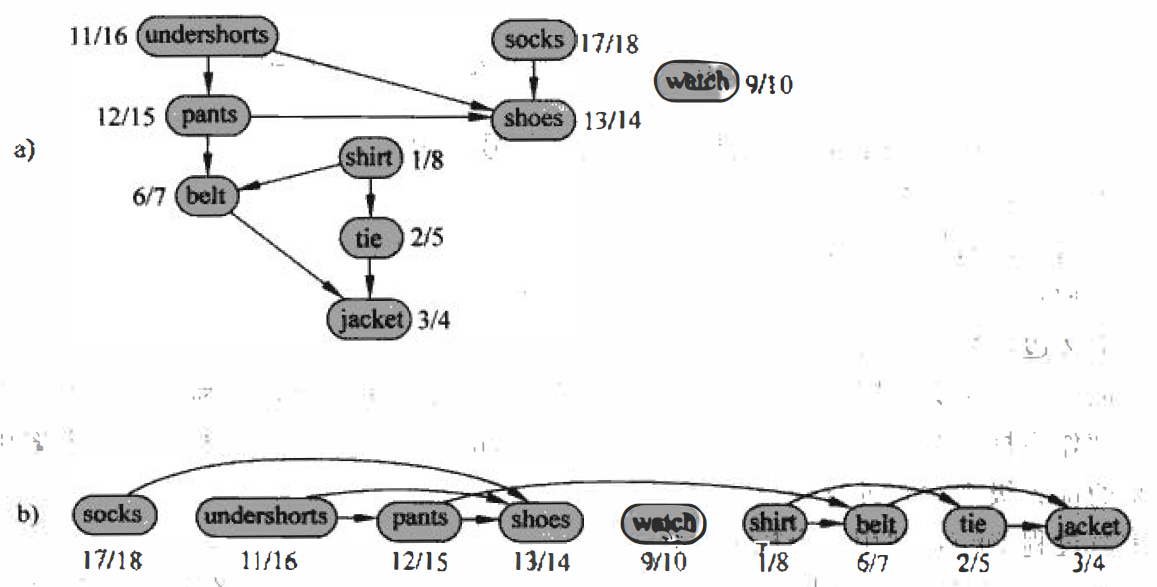
图 a 为 Bumstead 教授对他所穿的衣服进行了拓扑排序
每一条有向边 (u,v) 都意味若必须先穿衣服 u 再穿衣服 v
深度优先搜索中的发现和完成时间都在每个顶点的旁边示出
图 b 为 经过拓扑排序后的同一图形
图中的各个顶点按照完成时间的递降顺序从左向右排列,注意所有的有向边都是从左指向右的拓扑排序的实现
为了说明如何得到一个有向无环图的拓扑排序,我们首先需要了解有向图节点的入度(indegree)和出度(outdegree)的概念:
- 入度:设有向图中有一节点 \(v\),其入度即为当前所有从其他节点出发,终点为 \(v\) 的的边的数目。也就是所有指向 \(v\) 的有向边的数目。
- 出度:设有向图中有一节点 \(v\),其出度即为当前所有起点为 \(v\),指向其他节点的边的数目。也就是所有由 \(v\) 发出的边的数目。
在了解了入度和出度的概念之后,再根据拓扑排序的定义,我们自然就能够得出结论:要想完成拓扑排序,我们每次都应当从入度为 0 的节点开始遍历。因为只有入度为 0 的节点才能够成为拓扑排序的起点。否则根据拓扑排序的定义,只要一个节点 \(v\) 的入度不为 0,则至少有一条边起始于其他节点而指向 \(v\),那么这条边的起点在拓扑排序的顺序中应当位于 \(v\) 之前,则 \(v\) 不能成为当前遍历的起点。
由此我们可以进一步得出一个改进的深度优先遍历或广度优先遍历算法来完成拓扑排序。
广度优先算法实现拓扑排序
广度优先算法实现拓扑排序需要多保存每一个节点对应的入度(普通遍历算法只需要保存节点之间的关系),并在遍历的每一层选取入度为 0 的节点开始遍历(普通遍历算法则可以从该吃呢个任意一个节点开始遍历)。这个算法描述如下:
- 保存每一个节点与其他节点之间的关系,可以使用邻接表或者哈希表
- 计算并保存每一个节点的入度,可以使用数组
- 遍历选取入度为 0 的节点,并将该节点加入队列
- 取队列中的节点,加入排序结果列表,并将该节点的子节点的入度减 1
- 重复步骤 5,直到队列为空
- 如果排序结果列表和节点总数相同,代表遍历完了所有节点,否则说明有节点没有遍历到
- 如果遍历完所有的节点,则排序结果列表即为当前图的拓扑排序
- 如果无法遍历完所有的节点,则意味着当前图不是有向无环图,不存在拓扑排序
拓扑排序题目解析
207. 课程表
练习
- 「力扣」第 207 题:课程表(中等)
- 「力扣」第 210 题:课程表 II(中等)
- 「力扣」第 301 题:最小高度树(中等)
- 「力扣」第 802 题:找到最终的安全状态(中等)
- 「力扣」第 1203 题:项目管理(困难)
- 「力扣」第 630 题:课程表 III(困难)
- 「力扣」第 329 题:矩阵中的最长递增路径(困难)
- 「力扣」第 1245 题:树的直径(中等)
- 「力扣」第 444 题:序列重建(中等)
- 「力扣」第 1136 题:平行课程(困难)
- 「力扣」第 269 题:火星词典(困难)