数据结构与算法 - 矩阵快速幂

发表于 2020-10-05 更新于 2021-11-07 分类于数据结构与算法

转载说明

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/dynamic-programming-2-plus/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

矩阵快速幂是一种基础算法，本身与动态规划没有关系，但常用于优化线性递推关系的计算，并且其思路比较固定，本章将矩阵快速幂做基础介绍。

动态规划主要用于解决两类问题，一类是优化问题，求最优解，另一类是组合计数，求方案数。矩阵快速幂主要用在第二类，即组合计数，求方法数这类问题，可以将时间复杂度从 O(N) 降到 O(logN)。

快速幂

==50. Pow(x, n)==

快速幂的推导

不求 \(a^{n}\) 而是求 \(a^{\frac{n}{2}}\)，然后先不求 \(a^{\frac{n}{2}}\), 而是先求 \(a^{\frac{n}{4}}\)...

对以上思路最直接的实现方式是递归, 代码如下：

double _myPow(double x, long long n)
{
    if (n == 0)
        return 1;
    if (n < 0)
        return 1 / _myPow(x, -n);
    double mid = _myPow(x, n / 2);
    if (n & 1)
        return mid * mid * x;
    return mid * mid;
}

此外还有另外一个代码实现技巧：二进制分解，n -> 1, 2, 4, 8, 16, 32. n 可以分解为 2 的幂次的和。例如 13 = 8 + 4 + 113=8+4+1，求 \(a^{13}\) 需要求 \(a^{8}\), \(a^{4}\), \(a^{1}\) 可以用变量存 \(a^{1}\), \(a^{2}\), ..., \(a^{n - 1}\)，如果当前幂次是 n 需要的，则加到结果中。如何判断当前幂次是否需要，可以用位掩码来决定，即下面代码中的 n&1。

int quickpower(int a, int n)
{
    // a==0 && n==0 特判
    int ans = 1; // n = 0 时候不进循环
    while(n)
    {
        if(n & 1) ans *= a;
        a *= a;
        n >>= 1;
    }
    return ans;
}

矩阵快速幂

矩阵快速幂的推导

矩阵快速幂与快速幂的思想是一致的：求矩阵的幂 \(A^{n}\) 的时候，先不求 \(A^{n}\)，而是先求 \(A^{\frac{n}{2}}\)，然后先不求 \(A^{\frac{n}{2}}\)，而是先求 \(A^{\frac{n}{4}}\), ...

以上思路同样可以用二进制分解加位掩码来实现, 只是当某个位掩码为 1 表示该位需要的时候, 做的是快速幂做的是乘法，矩阵快速幂做的是矩阵乘法。

while(n)
{
    if(n & 1)
        ans = ans * A; // 这一步是矩阵的乘法
    A = A * A;
    n >>= 1;
}

矩阵快速幂的代码模板

实现矩阵快速幂，可以先写一个 struct Matrix 表示矩阵，之后的乘法，求幂都是针对这个类的运算。

其中用一个二维数组做数据成员，一个 init() 方法，将矩阵初始化为单位阵 (相当于 \(A^{0}\)) 的结果。然后重载 * 和 ^ 分别表示矩阵乘法和矩阵快速幂。代码如下：

其中 M 表示方阵的行数。

using ll = long long;
const int M = 2;

struct Ma
{
    int a[M][M];
    Ma()
    {
        memset(a, 0, sizeof(a));
    }

    void init() // 复位为单位阵
    {
        a[0][0] = a[1][1] = 1;
        a[0][1] = a[1][1] = 0;
    }

    Ma operator*(const Ma& B) const
    {
        Ma ans;
        for(int i = 0; i < M; ++i)
            for(int j = 0; j < M; ++j)
                for(int k = 0; k < M; ++k)
                    ans.a[i][j] += a[i][k] * B.a[k][j];
        return ans;
    }

    Ma operator^(int n) const
    {
        Ma ans;
        ans.init();
        Ma A = *this; // 拷贝一个出来用于自乘
        while(n)
        {
            if(n & 1)
                ans = ans * A;
            A = A * A;
            n >>= 1;
        }
        return ans;
    }
};

矩阵快速幂的适用问题

矩阵快速幂主要用于线性的递推型计数问题，以及一些动态规划中状态转移方程是线性递推关系的时候。有一些计数问题，通过对 n 比较小的情况进行手动推导，发现规律，可以猜想出递推关系。如果这个递推关系是线性，那么它可以转换成矩阵求幂问题，进而可以用矩阵快速幂加速。

例如斐波那契问题，即力扣第 70 题

【70. 爬楼梯】

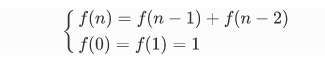
我们会思考是否可以构造一个矩阵 A，使得：

\[\begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix}\begin{bmatrix} f(0) \\ f(1) \end{bmatrix} = \begin{bmatrix} f(1) \\ f(2) \end{bmatrix}\]

通过一些推导，可以得到 \(A = \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\)，此关系可以继续推导下去，直到推出 \(\begin{bmatrix} f(n) \\ f(n + 1) \end{bmatrix}\)

最终可以得到：

\[\begin{bmatrix} f(n) \\ f(n + 1) \end{bmatrix} = A^{n}\begin{bmatrix} f(0) \\ f(1) \end{bmatrix} = {\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}}^{n}\begin{bmatrix} f(0) \\ f(1) \end{bmatrix}\]

推出以上公式之后就可以用套矩阵快速幂的算法求 \(A^{n}\) 了，此过程时间复杂度为 \(O(M^{3}logN)\)，M 为方阵的行数。

其它的线性递推关系均可以这样做：先找规律得到递推关系，然后将递推关系变为矩阵的形式，套矩阵快速幂。

例如：\(f(n) = 3f(n - 1) + 6f(n - 2) - 7f(n - 3)\)，的递推关系，可以变为矩阵形式

\[\begin{bmatrix} f(1) \\ f(2) \\ f(3) \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -7 & 6 & 3 \end{bmatrix}\begin{bmatrix} f(0) \\ f(1) \\ f(2) \end{bmatrix}\]

在上一章中的 16 道练习题中，部分题目的递推关系是线性的，进而可以用矩阵快速幂来做，尝试判断哪些题目可以用矩阵快速幂做，并用矩阵快速幂解决这些问题，加深对本节的理解。

何照江的博客