这一章将会介绍线性动态规划的相关概念和经典问题，并给出一些练习题供大家演练。

用动态规划解决问题的过程有以下几个关键点：状态定义，状态的转移，初始化和边界条件。

状态定义 就是定义子问题，如何表示目标规模的问题和更小规模的问题。例如常见的方法：定义状态 dp[n]，表示规模为 n 的问题的解，dp[n - 1] 就表示规模为 n - 1 的子问题的解。在实战中 dp[n] 的具体含义需要首先整理清楚再往下做。

状态转移 就是子问题之间的关系，例如定义好状态 dp[n]，此时子问题是 dp[n-1] 等，并且大规模的问题的解依赖小规模问题的解，此时需要知道怎样通过小规模问题的解推出大规模问题的解。这一步就是列状态转移方程的过程。一般的状态转移方程可以写成如下形式

dp[n] = f(dp[i]) 其中 i < n

按照状态定义和状态转移的常见形式，可以对动态规划进行分类，可以参考上一章的内容。

其中线性动态规划的主要特点是状态的推导是按照问题规模 i 从小到大依次推过去的，较大规模的问题的解依赖较小规模的问题的解。

这里问题规模为 i 的含义是考虑前 i 个元素 [0..i] 时问题的解。

线性动态规划简介

线性动态规划的主要特点是状态的推导是按照问题规模 i 从小到大依次推过去的，较大规模的问题的解依赖较小规模的问题的解。

这里问题规模为 i 的含义是考虑前 i 个元素 [0..i] 时问题的解。

状态定义：

dp[n] := [0..n] 上问题的解

状态转移：

dp[n] = f(dp[n-1], ..., dp[0])

从以上状态定义和状态转移可以看出，大规模问题的状态只与较小规模的问题有关，而问题规模完全用一个变量 i 表示，i 的大小表示了问题规模的大小，因此从小到大推 i 直至推到 n，就得到了大规模问题的解，这就是线性动态规划的过程。

按照问题的输入格式，线性动态规划解决的问题主要是单串，双串，矩阵上的问题，因为在单串，双串，矩阵上问题规模可以完全用位置表示，并且位置的大小就是问题规模的大小。因此从前往后推位置就相当于从小到大推问题规模。

线性动态规划是动态规划中最基本的一类。问题的形式、dp 状态和方程的设计、以及与其它算法的结合上面变化很多。按照 dp 方程中各个维度的含义，可以大致总结出几个主流的问题类型，见后面的小节。除此之外还有很多没有总结进来的变种问题，小众问题，和困难问题，这些问题的解法更多地需要结合自己的做题经验去积累，除此之外，常见的，主流的问题和解法都可以总结成下面的四个小类别。

单串

单串 dp[i] 线性动态规划最简单的一类问题，输入是一个串，状态一般定义为 dp[i] := 考虑 [0..i] 上，原问题的解，其中 i 位置的处理，根据不同的问题，主要有两种方式：

• 第一种是 i 位置必须取，此时状态可以进一步描述为 dp[i] := 考虑 [0..i] 上，且取 i，原问题的解；
• 第二种是 i 位置可以取可以不取

大部分的问题，对 i 位置的处理是第一种方式，例如力扣：

• 70 爬楼梯问题
• 801 使序列递增的最小交换次数
• 790 多米诺和托米诺平铺
• 746 使用最小花费爬楼梯

线性动态规划中单串 dp[i] 的问题，状态的推导方向以及推导公式如下：

依赖比 i 小的 O(1) 个子问题

dp[n] 只与常数个小规模子问题有关，状态的推导过程 dp[i] = f(dp[i - 1], dp[i - 2], ...)。时间复杂度 O(n)，空间复杂度 O(n) 可以优化为 O(1)，例如上面提到的 70, 801, 790, 746 都属于这类。

如图所示，虽然绿色部分的 dp[i-1], dp[i-2], ..., dp[0] 均已经计算过，但计算橙色的当前状态时，仅用到 dp[i-1]，这属于比 i 小的 O(1) 个子问题。

例如，当 f(dp[i-1], ...) = dp[i-1] + nums[i] 时，当前状态 dp[i] 仅与 dp[i-1] 有关。这个例子是一种数据结构前缀和的状态计算方式，关于前缀和的详细内容请参考下一章。

依赖比 i 小的 O(n) 个子问题

dp[n] 与此前的更小规模的所有子问题 dp[n - 1], dp[n - 2], ..., dp[1] 都可能有关系。

状态推导过程如下：

dp[i] = f(dp[i - 1], dp[i - 2], ..., dp[0])

依然如图所示，计算橙色的当前状态 dp[i] 时，绿色的此前计算过的状态 dp[i-1], ..., dp[0] 均有可能用到，在计算 dp[i] 时需要将它们遍历一遍完成计算。

其中 f 常见的有 max/min，可能还会对 i-1,i-2,...,0 有一些筛选条件，但推导 dp[n] 时依然是 O(n) 级的子问题数量。

例如：

• 139 单词拆分
• 818 赛车

以 min 函数为例，这种形式的问题的代码常见写法如下

for i = 1, ..., n
    for j = 1, ..., i-1
        dp[i] = min(dp[i], f(dp[j])

时间复杂度 \(O(n^{2})\)，空间复杂度 O(n)

单串相关练习题

• 最经典单串 LIS 系列
  • 最长递增子序列
  • 最长递增子序列的个数
  • 俄罗斯套娃信封问题
• 最大子数组和系列
  • 最大子序和
  • 乘积最大子数组
  • 环形子数组的最大和 —— 环形数组的处理
  • 面试题 17.24 最大子矩阵 —— 思路类似一维的最大子数组和
  • 矩形区域不超过 K 的最大数值和 —— 在上一题基础上加了一个 K
• 打家劫舍系列
  • 打家劫舍
  • 打家劫舍 II
  • 删除与获得点数
  • 3n 块披萨
• 变形：需要两个位置的情况
  • 最长的斐波那契子序列的长度
  • 最长等差数列
• 与其它算法配合
  • 形成字符串的最短路径 —— DP + 二分，贪心
  • 最大整除子集 —— 先对数组排序
• 其它单串 dp[i] 问题
  • 最长有效括号
  • 等差数列划分
  • 解码方法
  • 分割回文串 II
  • 比特位计数
  • 使序列递增的最小交换次数
  • 最低加油次数
  • 两个字符串的删除操作

带维度单串

单串的问题，子问题仅与位置 i 有关时，就形成单串 dp[i] 的问题。在此基础上，如果子问题还与某种指标 k 有关，k 的物理意义比较常见的有长度，个数，次数，颜色等，则是另一大类问题，状态通常写成 dp[i][k]。其中 k 上可能有二分，贪心等算法.

当 i 变小时，形成小规模子问题，当 k 变小时，也形成小规模子问题，因此推导 dp[i][k] 时，i 和 k 两个维度分别是一个独立的单串 dp[i] 问题。推导 k 时，k 可能与 k - 1,...,1 中的所有小规模问题有关，也可能只与其中常数个有关，参考单串 dp[i] 问题中的两种情况。

例如 256. 粉刷房子 ，其中 k 这一维度的物理意义是颜色推导 k 时，k 与 k - 1,...,1 中的所有小规模问题有关，则 k 这一维度的时间复杂度为 \(O(K^{2})\)

单串 dp[i][k] 的问题，推导状态时可以先枚举 k，再枚举 i，对于固定的 k，求 dp[i][k] 相当于就是在求一个单串 dp[i] 的问题，但是计算 dp[i][k] 时可能会需要 k-1 时的状态。具体的转移需要根据题目条件确定。参考 813。

矩阵上的 dp[i][j] 这类问题中也有可能会多出 k 这个维度，状态的定义就是 dp[i][j][k]，例如

• 576 出界的路径数
• 688 “马” 在棋盘上的概率

带维度经典问题

以下将涉及到的知识点对应的典型问题进行讲解，题目和解法具有代表性，可以从一个问题推广到一类问题。

==【813. 最大平均值和的分组】==

我们将给定的数组 A 分成 K 个相邻的非空子数组 ，我们的分数由每个子数组内的平均值的总和构成。计算我们所能得到的最大分数是多少。 注意我们必须使用 A 数组中的每一个数进行分组，并且分数不一定需要是整数。

输入是单串，但是有一个额外的次数的指标 k。在这种情况下，第一步是考虑单串 dp[i] 的子问题拆分方式：枚举子数组的起点来拆分子问题。

设计状态 dp[i] := [i..n-1] 上原问题的解，即 [i..n-1] 上分成 K 个相邻的非空子数组可得的最大分数

第二步是将额外的指标 K 作为一个维度加到状态里　dp[i][k] := [i..n-1] 上原问题的解，即 [i..n-1] 上分成 k 个相邻的非空子数组可得的最大分数

在推导状态时，先枚举 k，对于固定的 k，枚举 i ，枚举 i 时，相当于是在推导一个单串 dp[i] 的问题，但是计算 dp[i][k] 时需要用到 k-1 时的状态，这个区别在 2-1-4 中也有讨论。

由于 i 枚举的是起点，因此 i 越小的时候，子问题规模越大，需要从 n-1 到 0 枚举。

上面提到，固定 k 时，枚举 i ，相当于是在推导一个单串 dp[i] 的问题，这个问题在计算 i 的时候，需要此前已经计算的所有状态，即 i+1, i+2, ..., n-1。这相当于 2-1-1 中的第二种情况，但区别是这里有 k 这一个额外指标影响状态的推导。

对于区间 [i..n-1]，若分出了区间 [i,j-1], 则在区间 [j..n-1] 上分 k - 1 个区间，就可以将 [i..n-1] 分成 k 个区间。而 [i+1, .., n-1] 均有可能是这个 j。因此枚举这些 j ，将 [j, n-1] 上分 k-1 份的结果 dp[j][k-1] 加上 [i..j-1] 上的平均追 avg(i, j-1) 就得到了当前待计算状态 dp[i][k]。

结合题目条件，这个单串 dp[i][k] 的问题，状态的推导方向，以及推导公式如下:

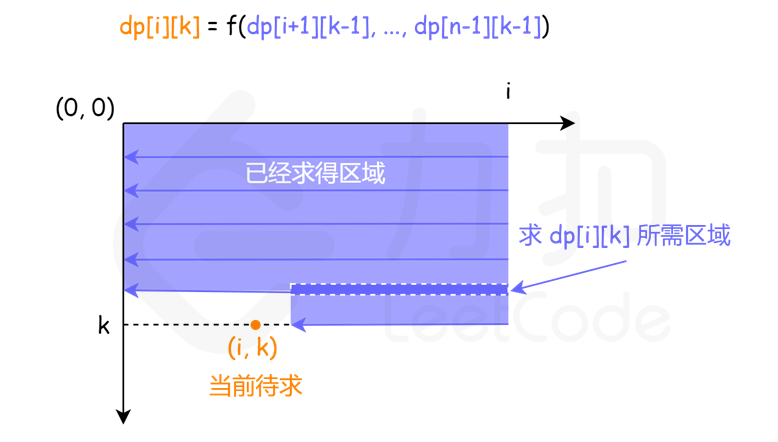
按照以上的分析，状态的转移方程可以写出来，如下：

\[ dp[i][k] = min_{j} dp[j][k-1] + avg(i, j-1)\ 其中 j 取 [i+1,..,n−1] 取较小值 \]

其中 \(avg(i, j)\)，是求子串 (i, j) 上的平均值，其中中间的一步求 \(sum(i, j)\) 可以用前缀和实现。前缀和的内容参考下一章。

带维度单串相关练习题

• 带维度单串 dp[i][k]
  • 最大平均值和的分组 —— k 是个数
  • 鸡蛋掉落 —— k 是次数，k 上有二分
  • 粉刷房子 —— k 是颜色
  • 粉刷房子 II —— k 是颜色
  • 奇偶跳 —— k 表示当前的奇偶状态
  • 青蛙过河 —— k 表示上一步的跳的步数
  • 安排邮筒 —— k 是个数，前缀和维护状态转移时的查询
  • 抛掷硬币 —— k 是个数
  • 分割数组的最大值 —— k 是份数
  • 给房子涂色 III —— 有两个指标 k 颜色；t 街区数
• 股票系列
  • 买卖股票的最佳时机
  • 买卖股票的最佳时机 II
  • 买卖股票的最佳时机 III
  • 买卖股票的最佳时机 IV
  • 最佳买卖股票时机含冷冻期
  • 买卖股票的最佳时机含手续费

双串

有两个输入从串，长度分别为 m, n，此时子问题需要用 i, j 两个变量表示，分别代表第一个串和第二个串考虑的位置 dp[i][j]:= 第一串考虑 [0..i]，第二串考虑 [0..j] 时，原问题的解

较大规模的子问题只与常数个较小规模的子问题有关，其中较小规模可能是 i 更小，或者是 j 更小，也可以是 i，j 同时变小。

其中一种最常见的状态转移形式：推导 dp[i][j] 时，dp[i][j] 仅与 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]，例如

• 72 编辑距离
• 712 两个字符串的最小 ASCII 删除和

线性动态规划中双串 dp[i][j] 的问题，状态的推导方向以及推导公式如下：

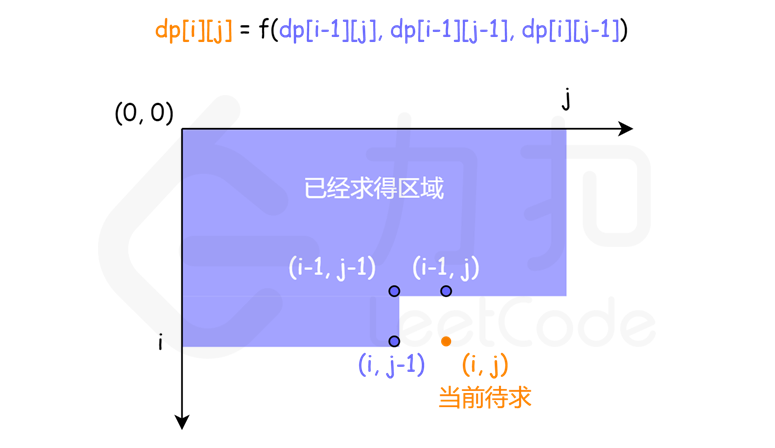
如图所示，绿色部分的 dp[i-1 ~ 0][j-1 ~ 0] 均已经计算过，但计算橙色的当前状态时，仅用到 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]，即比 i, j 小的 O(1)O(1) 个子问题。

这种形式的线性 DP 的代码常见写法

for i = 1..m
    for j = 1..n
        dp[i][j] = f(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])

时间复杂度 O(mn)，空间复杂度 O(mn)

以上是 O(1) 转移的情况，即计算 dp[i][j] 时，虽然绿色部分的子问题均已经计算完，但只需要用到 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]。也可能出现更高复杂度的转移，类似单串中依赖比 i 小的 O(n) 个子问题的况。

双串相关练习题

• 最经典双串 LCS 系列
  • 最长公共子序列
  • 两个字符串的最小 ASCII 删除和 —— LCS，len 和 ascii 各一个 dp
  • 最长重复子数组 —— 最长公共子串，注意与最长公共子序列的区别
• 字符串匹配系列
  • 编辑距离
  • 通配符匹配
  • 正则表达式匹配
• 其它双串 dp[i][j] 问题
  • 交错字符串
  • 不同的子序列
• 带维度双串 dp[i][j][k]
  • 扰乱字符串

矩阵

输入是一个矩阵，宽和高分别为 m, n，用两个维度表示问题规模 dp[i][j]:= 第一维度考虑 [0..i], 第二维度考虑 [0..j]，原问题的解

这样的状态定义，i 减小，j 减小均可以得到小规模子问题，两个维度均从小到大按顺序推，单独看各自维度，均是一个类似 上 的单串 dp[i] 问题，同样有单串中的两种情况，即转移时要考虑 O(1) 个小规模子问题，和转移时要考虑 O(n) 个子问题。

两个维度均只需考虑 O(1)O(1) 个子问题是最简单的情况，一般 dp[i][j] 就只与 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 有关，例如 64，但是也有可能出现需要其它位置的状态的情况，需要结合题目分析，这里分析的计算 dp[i][j] 需要哪些状态，决定了状态推导的方向。

线性动态规划中矩阵 dp[i][j] 的问题，状态的推导方向以及推导公式与双串 dp[i][j] 相同，但是物理意义不一样，且求 dp[i][j] 时所需的子问题的变化相对更多。

矩阵相关练习题

• 矩阵 dp[i][j]
  • 三角形最小路径和
  • 最小路径和
  • 地下城游戏
  • 下降路径最小和
  • 最大正方形
  • 下降路径最小和 II
• 矩阵 dp[i][j][k]
  • 最大矩形
  • 矩形区域不超过 K 的最大数值和 —— k 为宽度
  • 最大子矩阵 —— 思路类似一维的最大子数组和
  • 切披萨的方案数 —— 需要二维前缀和判断两个状态之间能否转移

线性动态规划总结

线性动态规划是动态规划中最基础的一类，它的状态一般物理意义很明确，易于分析。在初学动态规划时，通过线性动态规划的大量练习，可以不断加深动态规划的概念理解，例如动态规划中最重要的三个概念：最有子结构，重复子问题，无后效性。下面对动态规划的三个基本概念做个简要回顾，在线性动态规划的题目练习中可以不断地加深理解，之后再学习其它的动态规划类型就会容易很多。

最优子结构：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构。 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。 重复子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势） 线性动态规划是动态规划中变化最多的一类。

首先线性动态规划针对的问题是最常见的数组，字符串，矩阵等，这三种数据结构本身就是线性的，因此出现这些类型的输入的时候，如果要用到动态规划，首先考虑线性动态规划就很合理了，因此很多问题不论最后正解是不是线性动态规划，都会首先想一下线性动态规划是否可行。

其次由于大部分问题的数据都是以这三种形式给出的，因此题目的变化会非常多，很多常见的输入形式以及问题都非常经典，都存在经典的状态设计。因此不考虑一些比较 Trick 的解法，仅仅是经典问题的经典状态设计，就比其它种类的动态规划问题多很多了。

例如单个数组或字符串上设计一维状态，两个数组或字符串上设计两维状态，以及矩阵上设计两维状态等等，同时以上三种情况的状态设计都有可能再加上额外的指标的状态，就是前面例题中的 k，这里面变化就很多了，比如有的题目在 k 这一维上要使用二分，贪心的策略，有的题目需要 DP 状态与数据结构配合来解决问题。

除此之外还有一类问题没有显式的数组，字符串，但是在求解的时候依然满足前面提到的动态规划三条基本概念，可以用动态规划求解，这种问题通常也是线性动态规划。如此多的变化仅仅本小节例举的题目是远远不够的，下一小节是线性动态规划的练习题，涉及到对线性动态规划的更多的变化。

推荐阅读顺序

1. 数据结构与算法 - 动态规划（简介）
2. 数据结构与算法 - 动态规划（线性动态规划）
3. 数据结构与算法 - 动态规划（前缀和）
4. 数据结构与算法 - 动态规划（区间动态规划）
5. 数据结构与算法 - 动态规划（背包问题）
6. 数据结构与算法 - 动态规划（状态压缩）
7. 数据结构与算法 - 动态规划（计数问题）
8. 数据结构与算法 - 矩阵快速幂
9. 数据结构与算法 - 动态规划（数位动态规划）